Table of Content
- What is Thermal Conductivity?
- Thermal Conductivity for Homogenous and Heterogeneous Materials
- Thermal Conductivity in Isotropic and Anisotropic Materials
- Variation of Thermal Conductivity with Temperature
- Effect of Alloying on Thermal Conductivity
- Effect of Density and Wetness on Thermal Conductivity
- Unit of Thermal Conductivity
AFRILCATE
What is Thermal Conductivity?
Thermal conductivity refers to how highly or poorly a medium conducts heat.
It is an indication of the rate at which heat energy is transmitted through a medium by conduction process.
The symbol for thermal conductivity is k.
In actual practices, the thermal conductivity varies from point to point within the material.
For instance,Ā if kx , ky , and kz are thermal conductivities in x, y and z directions respectively, then in some cases,
(kx )1 ā (kx)2
(ky )1 ā (ky)2
The difference can be of negligible value and in such cases, the thermal conductivity is assumed to have the same value throughout the material. This depicts ideal cases.Ā Ā
In addition, the value of k for heat conduction in a given direction may be different for heat conduction in another direction. i.e.
kX ā ky ā kZ
Thermal conductivity varies from material to material.
They are generally high for solids, intermediate for liquids and low for gasses, as shown below
Kgas is in the range of 0.008 ā 0.08 W/mKĀ Ā Ā Ā Ā Ā Ā Ā (for gases)
Kliquid is in the range of 0.08 ā 0.8 W/mKĀ Ā Ā Ā Ā Ā Ā Ā (for liquid)
Ksolid is in the range of 0.8W/mK ā higher W/mKĀ Ā (for solids)
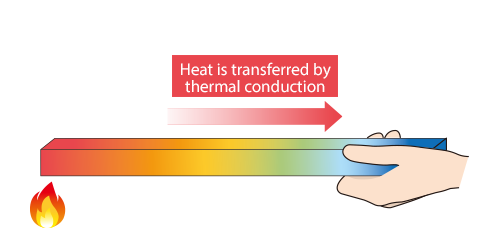
Heat is thermally conducted along the rod.
Thermal Conductivity for Homogenous and Heterogeneous Materials
If k has the same value throughout a material medium, then the material is said to be homogeneous;
but if the thermal conductivity varies from point to point within the material, the material is said to be homogeneous.
i.e. for a given material medium,
k1 = k2 Ā Ā Ā Ā Ā Ā homogeneous material
k1 ā k2Ā Ā Ā Ā Ā Ā Ā heterogeneous material
Solids may consist of a fine mixture of different materials making them heterogeneous.
Also, porous substances like fired clay, cork, foam, etc are heterogeneous.
Thermal conductivity is also a function of temperature.
This means that a material can be heterogeneous if it exists at a non-uniform temperature.
As mentioned earlier, the variation of k in many engineering materials may be so small that the differences are assumed to be negligible.
In such cases, the material is assumed to be homogeneous.
Examples of homogeneous materials are Cu, Zn, H2O, air and aluminumĀ (at uniform temperature).
Thermal Conductivity in Isotropic and Anisotropic Material
An Isotropic material is a material whose thermal conductivity at any location is the same in all directions.
But if k at a point varies with direction, the material is said to be anisotropic.
| kX = ky = kZ = k ā¦ā¦ā¦ā¦ if isotropic |
kX1 = ky1 = kZ1 = k1 āāat location 1 (isotropic)
kX2 = ky2 = kZ2 = k2 āāat location 2 (isotropic)
but:
| kX ā Ā ky ā Ā kZĀ ā¦ā¦ā¦ā¦ ifĀ anisotropic |
Examples of anisotropic materials are wood, glass other fibrous materials.
Many engineering materials can be assumed to be isotropic.
Water, copper, aluminum and materials with directionally invariant structures are isotropic.
copper is an isotropic material
Variation of Thermal Conductivity with Temperature
Thermal conductivity for crystalline materials and liquids decreases with temperature.
Thermal conductivity for gas and amorphous substances (like glass and rubber) increases with temperature.
Effect of Alloying on Thermal Conductivity
For alloys, the thermal conductivity may be in-between those of the constituents or even less than that of any of the material.
The alloy nickel-silver contains
Cu ā 64%Ā k = 381Ā W/mKĀ Ā atĀ 20ā¦C
Ni ā 18%Ā k = 90Ā Ā W/mKĀ atĀ 20ā¦C
Zn ~ 17%Ā k = 112.1Ā W/mKĀ atĀ 20ā¦C
But k for nickel ā silver at 20ā¦C is 31.3 W/mK, which is below the values for all the constituents.
alloying metals
Effect of Density and Wetness on Thermal Conductivity
For any material, k increases with increasing density and with increasing wetness.
Unit of Thermal Conductivity
The unit of thermal conductivity is obtained from Fourierās law.
Fourierās law states that:
āThe heat flow rate per unit cross-sectional area A, is proportional to the average temperature gradient and itās in the direction of decreasing temperatureā.Ā
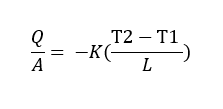
Therefore,
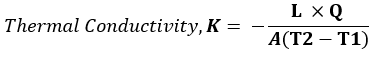
Where:
Ā L = length or thickness of the material (m);
Q = heat flow (W)
A = surface area of material(m2),
T2 ā T1 = temperature difference (K or ā¦C)
Hence Unit of k = W/ mā¦CĀ Ā orĀ Ā Ā W/ mKĀ Ā Ā
